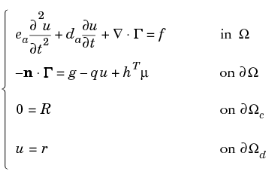The first line (equation) of Equation 16-1 is the PDE, which must be satisfied in
Ω. The second, third, and fourth equations are the boundary conditions, which must hold on
∂Ω. The second equation is a generalization of a
Neumann boundary condition. The third equation is a general
constraint, of which the
Dirichlet boundary condition on the fourth line is a special case.
The terms Γ,
f,
g,
q,
R, and
r are user-defined coefficients. They can be functions of the spatial coordinates, the solution
u, and the space derivatives of
u (see
PDE Interface Variables), as well as of other predefined and user-defined variables. The coefficients
f,
g,
q,
R, and
r are scalar, whereas
Γ is the
flux vector.
In practical applications, Γ typically represents the flux of a conserved quantity such as heat, charge, mass, or momentum. This flux is usually related in some empirical way, via a material law, to the gradient of the dependent variable. Therefore,
Γ is usually a vector whose components are functions of derivatives of the dependent variable. The flux vector can also contain terms that are proportional to a velocity field when there is convective transport of the conserved quantity present. The structure of
Equation 16-1 implies that the normal component of
Γ is continuous across any surface in the interior of the domain,
Ω.
In finite element terminology, the boundary condition on the second line of Equation 16-2, corresponding to a Neumann boundary condition, is called a
natural boundary condition, because it does not occur explicitly in the weak form of the PDE problem. In the PDE interfaces, the corresponding condition is called a
flux or
source, because it specifies the value of the numerical flux
Γ at the boundary.
Constraints and Dirichlet conditions are also known as essential boundary conditions in finite element theory, because they impose a restriction on the trial space, which is not part of the main equation. In the PDE interfaces, a distinction is made between Dirichlet boundary conditions and
constraints. The general constraint on line 3 of
Equation 16-2 specifies that an arbitrary expression is equal to zero on the boundary:
R = 0. The Dirichlet condition on line 4 of the same equation is a special case directly specifying the value of the dependent variable at the boundary:
u = r. This makes the constraint a more general boundary condition.
The term −hTμ in the generalized Neumann condition is a reaction term enforcing the constraint
R = 0. When reaction terms are applied symmetrically on all dependent variables,
but also other definitions are possible. The variable μ is a Lagrange multiplier, which is eliminated by the solvers when using standard constraints, and therefore does not normally appear explicitly in equations.