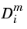
where ρi is the density and xi the mole fraction of species i. The diffusion hence depends on a single concentration gradient and is proportional to a diffusion coefficient . The diffusion coefficient describes the diffusion of species i relative to the remaining mixture and is referred to as the mixture-averaged diffusion coefficient. Equation 3-46 can be expressed in terms of mass fractions as

Assuming isobaric and isothermal conditions, the following expression for the mixture-averaged diffusion coefficient can be derived from the Maxwell-Stefan equations (Ref. 3):

The mixture-averaged diffusivities are explicitly given by be the multicomponent Maxwell-Stefan diffusivities Dik. As a consequence, no matrix inversion operation is required as for the Maxwell-Stefan diffusion model (when using four or more species). For low-density gas mixtures, the Dik components can be replaced by the binary diffusivities for the species pairs present.