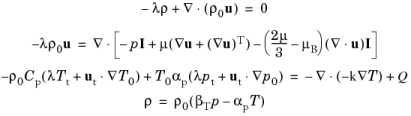where the eigenvalue is λ =
−iω. It is important to note that there is a difference between regular pressure acoustics and thermoviscous acoustics in terms of what modes can exist and which modes are found during an eigenfrequency study. In pressure acoustics only the pure acoustic modes exist; here the equations and assumptions made ensure this. In thermoviscous acoustics, on the other hand, the equations are formulated for all small signal components that can exist. This means that other nonacoustic modes also exist, that is, thermal and vorticity modes.
where λ is the eigenvalue. Typically, eigenvalues exist near the positive real axis, where
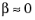
. These are exponentially decaying nonacoustic (nonoscillating) modes that stem from the thermal equation or the deviatoric part of the momentum equation (the nonpressure and nonvolume part of the stress tensor) also called the vorticity modes. The acoustic eigenvalues on the other hand lie close to the imaginary axis and are oscillating and slightly damped.