This model has been developed as a lowest-order, reasonable approximation to experimental data in Ref. 27 (see their Figure 9). It consists of a simple serial RCL circuit applied on a transducer area of At, and has the impedance

with At = 1.5 cm2, Rs = 9.0 N s m-1, Ls = 0.53×10-3 N s2 m-1 and Cs = 5.3×10-6 m N-1.

Four models related to the human ear have been included. These detailed and experimentally-verified circuit models describe parts of the human ear, as well as the entire human ear, see Ref. 28 to 30 for further details.

This impedance describes the acoustic radiation losses from the pinna (also known as the auricle, this is the visible part of the ear which is exterior to the head), see Figure 2-8. For cases where you model the ear canal explicitly using pressure acoustics, this boundary condition describes the acoustic losses from the outward acoustic radiation from the ear canal and into the surrounding air.

where Rpar = 7.0×106N s m-5, Lpar = 100 N s2 m-5, Cpar = 1.7×10-12 m5 N-1, Q = 6, R1 = R2 = Rpar, R3 = 2 Rpar, ω1 = 6000·2π Hz, ω1 = 9000·2π Hz and ω1 = 13000·2π Hz.

This model describes the impedance of the human ear drum and the entire inner ear, that is, the acoustic impedance experienced in the ear canal when looking into the ear drum, see Figure 2-9. The model equations are given in Equation 2-20 and Equation 2-21, and the parameter values in Table 2-8.

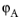
The parameter values are given in Table 2-8. Note that the value of is not reported in the papers Ref. 28 to 30, but has instead been read off during model implementation.

This model accounts for the acoustic losses associated with the ear canal and the entire human ear, see Figure 2-10. It does not include the radiation losses associated with the pinna, the visible part of the ear which is external to the head.

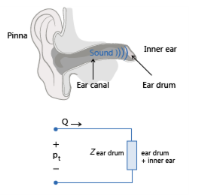
Here, Zeardrum is the eardrum impedance defined in Equation 2-21 and cij are the components of the ear canal two port C. The ear canal is treated as Ntot small segments each with length Δk and radius rk so its two port C is given by

In these expressions, γ is the ratio of specific heats, Γk is the propagation constant (“wave number”) of the kth ear canal segment which has the segment-specific attenuation αk,

is the Prandtl number expressed in terms of the specific hear Cp, dynamic viscosity μ, and thermal conductivity k. Notice that the papers presenting the model (Ref. 28 to 30) do not exactly specify which expression for the attenuation constants αk is being used, but only refer to Ref. 31. The expression above for αk is the most general expression taken from this paper. The values for Δk and rk are listed in Table 2-9.

The pressure at the eardrum peardrum is calculated whenever this impedance boundary condition is applied. This pressure is available in the plot group, and is calculated from the expression

where pt is the pressure on the boundary, cij are the coefficients of the ear canal two port C and Zear w/o pinna is the ear impedance; C and Zear w/o pinna are defined in Equation 2-22 and Equation 2-23 above.

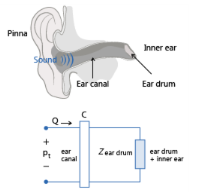
This model accounts for all acoustic losses associated with the entire human ear, both the internal parts as well as the pinna, the visible, external part of the ear on the head, see Figure 2-11. The model does not include any information about the directivity of the ear (the head related transfer functions, HRTFs) which depends on the ear geometry at higher frequencies. It is valid in the low frequency limit and for normal incidence on the ear. It is given by

where Zrad and Zear w/o pinna are given by Equation 2-19 and Equation 2-22 above.

The pressure at the eardrum peardrum is calculated whenever this impedance boundary condition model is applied. This pressure is calculated from Zear full using the expression