Pressure acoustic problems involve solving for the small acoustic pressure variations p (also named
p’ or
p1) on top of the stationary background pressure
p0. Mathematically, this represents a linearization (small parameter expansion) of the dependent variables around the stationary quiescent values.
where ρ is the total density,
p is the total pressure,
u is the velocity field,
s is the entropy,
M and
F represent possible source terms. In classical pressure acoustics, all thermodynamic processes are assumed to be reversible and adiabatic, that is, isentropic processes. The small parameter expansion is performed on a stationary fluid (
u0 =
0) of density
ρ0 (SI unit: kg/m
3) and at pressure
p0 (SI unit: Pa) such that:
where cs is recognized as the (isentropic) speed of sound (SI unit: m/s) at constant entropy
s. The last equation for the pressure time differential is derived from the entropy equation, for more details see
Theory Background for the Thermoviscous Acoustics Branch. For constant material parameters the last equation reduces to the usual relation
The subscript s is dropped in the following along with the subscript 0 on the background density
ρ0. Finally, rearranging
Equation 2-4, renaming the source terms, and dropping the subscript 1 yields the wave equation for pressure waves in a lossless medium
Here ρ (SI unit: kg/m
3) refers to the density, and
c (SI unit: m/s) denotes the speed of sound. In this general formulation of the scalar wave equation, the speed of sound and density may in general be space dependent, for example, through their dependency on the background temperature. The equation includes two optional source terms:
The combination ρc2 is called the
adiabatic bulk modulus, commonly denoted
Ks (SI unit: Pa). The bulk modulus is equal to the one over the adiabatic compressibility coefficient
βs = 1/
Ks = 1/
ρc2(SI unit: 1/Pa).
In Equation 2-5 both the speed of sound
c = c(
x) and the density
ρ = ρ(
x)
may be dependent on the spatial coordinates
x while they are independent of time, or only slowly varying in time (that is, at a time scale much slower than the variations in the acoustic signal). If both domain sources are set to zero and the density is constant in space, you can recover the standard wave equation
where ω =
2πf (rad/s)
is the angular frequency and
f (SI unit: Hz) is the frequency. Assuming the same harmonic time dependence for the source terms, the wave equation for acoustic waves reduces to an inhomogeneous Helmholtz equation
In this equation, the subscript “c” on the density and the speed of sound refers to that they may be complex valued. Lossy media, like porous materials or highly viscous fluids, can be modeled by using the complex-valued speed of sound and density. A selection of such fluid models is available in
The Pressure Acoustics, Frequency Domain Interface. The attenuation in these fluid models is frequency dependent in different ways, depending on the physical origin of the damping. A description of the different fluid models is given in
Theory for the Equivalent Fluid Models.
The damping term in Equation 2-7 is absent from the standard PDE formulations in the Pressure Acoustics, Transient interface, but it corresponds to a monopole domain source proportional to the time derivative of the pressure. This approach is, however, not used in the viscous and thermally conducting fluid models that contain damping for transient acoustics (see
Viscous Fluid Model,
Thermally Conducting Fluid Model, and
Thermally Conducting and Viscous Fluid Model). The physical origin of the damping corresponds here to a dipole-like source.
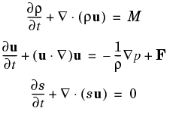
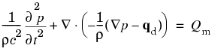 .
.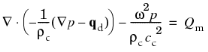 .
.