where Z is the inner circumference of the pipe and A = A(x,p,...) is the inner wetted cross-sectional area, u is the area-averaged mean velocity, which is also defined in the tangential direction u = uet, p is the mean pressure along the pipe, τw is the wall drag force, and F is a volume force. The gradient is taken in the tangential direction et. The term β is a flow profile correction factor relating the mean of the squared total velocity to the square of the mean velocity. Such that

are the local non-averaged parameters. Again p and u are the area-averaged dependent variables.

where A0 is often only function of x; however, A0 can be changed by external factors such as heating or structural deformation, thus the time dependency. The 1st order terms represent small perturbations on top of the background values (0th order). They are valid for

Moreover, the perturbations for the fluid density and cross-sectional area are expanded to first order in p0 in a Taylor series such that

where the subscript s refers to constant entropy; that is, the processes are isentropic. The relations for the fluid compressibility and the cross-sectional area compressibility are

Here, β0 is the fluid compressibility at the given reference pressure p0, the isentropic bulk speed of sound is denoted cs, and ρ0 is the fluid density at the given reference temperature and reference pressure. βA is the effective compressibility of the pipe’s cross-sectional A0 due to changes in the inner fluid pressure. The bulk modulus K is equal to one over the compressibility.

Inserting the above expansions into the governing equations (Equation 3-13 and Equation 3-14) and retaining only 1st-order terms yield the pipe acoustics equations including background flow. These are:

where c is the effective speed of sound in the pipe (it includes the effect due to the elastic properties of the pipe defined through KA). The bulk modulus for the cross-sectional area KA is given by the pipe material properties according to the so-called Korteweg formula (see Ref. 2). For a system with rigid pipe walls cs = c as KA tends to infinity.

Using the fact that the velocity is taken along the tangential direction et the governing equations are rewritten in terms of the scalar values u and p and projected onto the tangent. The 0 subscript is dropped on the density and area and the 1 subscript is also dropped on the dependent variables.

where 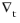is the tangential derivative, τw is the tangential wall drag force (SI unit: N/m2) and F is a volume force (SI unit: N/m3).

inserting this into the governing Equation 3-18 (and dropping the tilde) yields the equations solved in the Pipe Acoustics, Frequency Domain interface:

where is the angular frequency and f is the frequency.